Indirect Configuration Steam-to-Salt Heat Exchanger

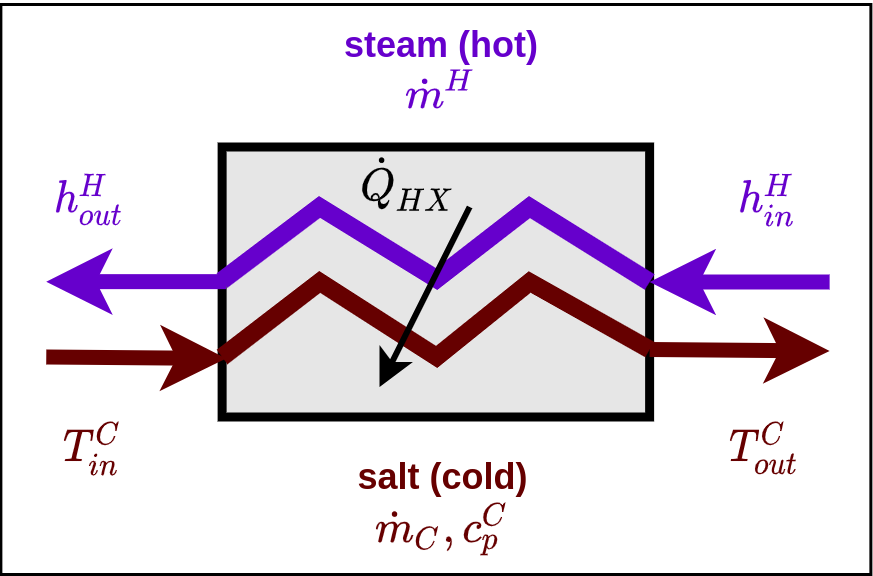
Heat exchanger diagram, based on White et al. (2021). Heat lost to surroundings assumed to be 0.

Hot Stream - Steam

Hot stream in this case is the fraction of steam coming from the LFR loop. The heat exchanged between the two streams can be written in terms of the hot stream properties as:

(1)\[\color{red}{\dot{Q}_{HX}} \color{black}{ = \dot{m}^H ( h^H_{in} - } \color{red}{h^H_{out}} \color{black}{).}\]

Unknown properties are highlighted in red. The superscript \({}^H\) represents the hot stream into the HX which is this case is the steam. For the steam, we have loop-up tables for enthalpy as a function of temperature and pressure. We assume that the steam inlet temperature, mass flow and pressure are known:

\[\begin{split}\begin{align} \dot{m}^H &= \text{calculated from } \texttt{nuclear_plant} \\ T^H_{in} &= 570 {}^\circ \text{C} \\ P^H_{in} &= 23.5 \text{MPa} \end{align}\end{split}\]

The enthalpies in Eq. 1 are therefore:

\[\begin{split}\begin{align} h^H_{in} &= f(T^H_{in}, P^H_{in}) \\ \color{red}{h^H_{out}} &= f(\color{red}{T^H_{out}} \color{black}{ , P^H_{in}) } \end{align}\end{split}\]

assuming no pressure drop across the HX. Outlet temperature conditions for the steam are not known ahead of this calculation.

Cold Stream - Molten Salt

Cold stream in this case involves the molten salt taken from cold tank and sent to hot tank of thermal energy storage (TES) system. The heat exchanged between the two streams can be written in terms of the cold stream properties as:

(2)\[\color{red}{\dot{Q}_{HX}} \color{black}{ = } \color{red}{\dot{m}^C} \color{black}{c^{\text{salt}}_P ( T^C_{out} - T^C_{in}).}\]

Based on the discussion in :ref:` the Model 2 outlet mixing guide <directTESoutletMixing>` we can make the assumption that the change in enthalpy of the molten salt is proportional to the specific heat of the fluid and change in temperature. We want to calculate the mass flow of the salt.

The known values here are:

\[\begin{split}\begin{align} T^C_{in} &= \text{calculated from } \texttt{tes_two_tank} \\ T^C_{out} &= 560 {}^\circ \text{C} \\ c^{\text{salt}}_P &= \text{calculated from } \frac{1}{2} (T^C_{out} + T^C_{in}) \end{align}\end{split}\]

Heat Exchanger Effectiveness

The effectiveness of the heat exchanger is written as

(3)\[\color{black}{\epsilon = } \frac{\color{red}{\dot{Q}_{HX}}}{\color{red}{\dot{Q}_{max}}}\]

where the maximum heat exchanged is defined under perfect heat exchange conditions. In this case, we use the minimum capacitance rate of the two fluids (assuming hot fluid has lower minimum capacitance rate). We also use the maximum difference in enthalpies:

(4)\[\color{red}{\dot{Q}_{max}} \color{black}{ = \dot{m}^H (h^H_{in} - h^H_{out,ideal} ).}\]

where

\[h^H_{out,ideal} = f(T^C_{in}, P^H_{in})\]

which implies that under these ideal conditions, the steam will exit the HX with the maximum temperature change. We then calculate the actual heat exchanged by combining Eq. 3 and Eq. 4 as

(5)\[\color{red}{\dot{Q}_{HX}} \color{black}{ = \epsilon \dot{m}^H (h^H_{in} - h^H_{out,ideal} ). }\]

Solving for Unknown Variables

The cold stream mass flow can be calculated by combining the Eq. 2 and Eq. 5 as:

\[\color{red}{\dot{m}^C} \color{black}{ = \frac{\epsilon \dot{m}^H (h^H_{in} - h^H_{out,ideal} )}{c^{\text{salt}}_P ( T^C_{out} - T^C_{in} )} }\]

The outlet temperature of the steam within the HX can be backed out by solving for \(\color{red}{\dot{Q}_{HX}}\) in Eq. 5 and substituting that into Eq. 1 to find:

\[\color{red}{h^H_{out}} \color{black}{ = h^H_{in} - \frac{\dot{Q}_{HX}}{\dot{m}^H } }\]

from which we can back out the temperature by through the steam tables

\[\color{red}{T^H_{out}} \color{black}{ = f^{-1}(h^H_{out}, P^H_{in} ) }\]